Okay, it’s 10pm of October 31st and I promised myself that I’d write another blog post by the end of the month, so let me try whip up something in a couple hours.

Introduction⌗

Depth-first search (DFS for short) is one of the most well-known graph algorithms in computer science. The algorithm looks something like:

dfs(u):
    for each edge u -> v:
        if v has not been visited before:
            dfs(v)

I wouldn’t really even call this an algorithm. It’s just a way in which you can traverse through a graph. Saying DFS is an algorithm is like saying for loops are algorithms.

(From now on, I’m going to assume you know a bit about graph theory, like what the words “graph”, “undirected”, “node”, “edge”, “tree”, “subtree” mean. If you want, you can look them up now.)

Anyway, depth-first search can be used in a lot of different ways, but today I want to focus on one common pattern that people use when they do DFS, that being DFS trees.

A DFS tree is formed when you perform DFS on a graph, and you look at which edges you recursed down when you did the DFS. In the above code example, any time we call dfs(v) from dfs(u), the edge u -> v goes in the DFS tree.

One cool property of DFS trees on undirected graphs is that any edges that do not get added to the DFS tree, must lead between a node and one of its ancestors.

Well, now that we have DFS trees, what should we do? Let’s use this on a competitive programming problem.

Problem: Icy Itinerary⌗

This problem is from the 2022 Nordic Collegiate Programming Contest. If you want to read the full problem, check out this link. Essentially, the short form of the problem is:

Given an undirected graph with nodes numbered $1$ to $N$, find an ordering of nodes $a_1, \dots, a_N$ such that $a_1 = 1$ and there exists at most one index $i$ such that, either

$a_{i-1}$ has an edge to $a_i$ but $a_i$ has no edge to $a_{i+1}$
$a_{i-1}$ has no edge to $a_i$ but $a_i$ has an edge to $a_{i+1}$.

Essentially, we want a sequence of nodes that looks like this:

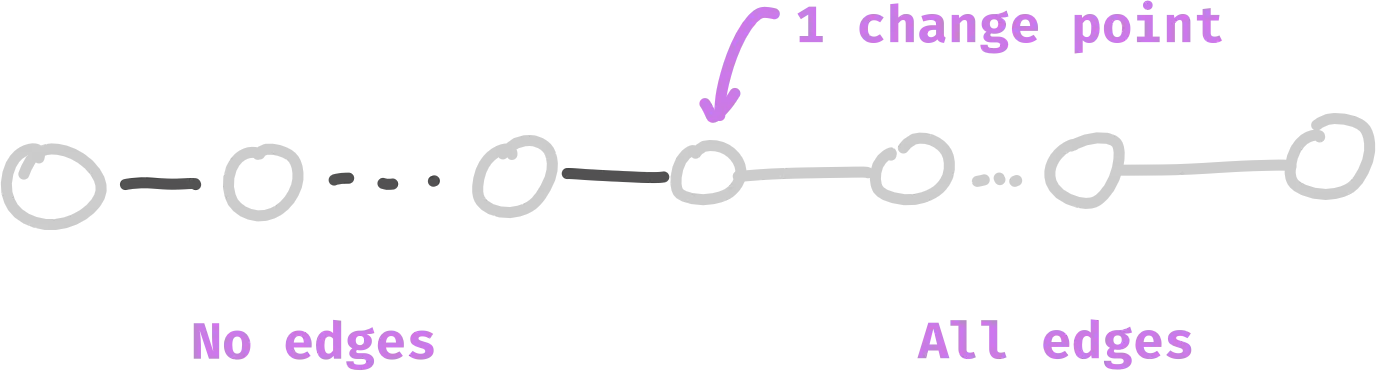
Spoiler warning⌗

I’m going to be spoiling the solution in a bit. This problem is a bit tricky, and there are a couple other solutions to this problem that I won’t be covering. If you want to think about this problem before I spoil the solution, please stop reading here. It’s quite likely that the solution you get will be completely different from mine!

Solution⌗

You back?

You ready?

Cool.

Let’s talk about DFS.

Truth be told, I couldn’t solve this problem without prompting from a friend. When I explained the problem to me, he asked me something like,

What if the problem gave you a tree instead of a graph?

That got me thinking… How would I solve it? Surely there exists a way to generalise to the graph case?

On a tree⌗

Let’s root the tree at node 1, since it’s going to have to go at the start. Well, sibling subtrees cannot have edges between them, so as long as I have a node with two child subtrees, then I’ll be able to produce most of the sequence by simply alternating nodes from the two subtrees.

Whatever’s left of the tree can only be a line, so we can just connect up the remaining nodes in a line to form the two parts of our sequence, right?

Okay, that was a bit handwavy. Let’s write out the construction in pseudocode:

combine(seq1, seq2):
    result = []
    while neither seq1 nor seq2 are empty:
        alternate adding elements in seq1 & seq2 to the end
    add the rest of the elements in the remaining list to the end
    return result

construct(node):
    sequence = []
    for each child node c:
        child_sequence = construct(c)
        sequence = combine(sequence, child_sequence)
    add n to back of sequence
    return sequence

(Notice how I used DFS in construct? :P)

Why does this work?

Well, if we have two sequences seq1 and seq2 that start with nodes that don’t have edges between them and end with nodes that have edges between them, the resulting sequence is only going to start having edges between adjacent pairs, when one of the sequences runs out.

This means that there can’t be two or more change points, because we don’t add any new change points. It might be more clear to draw this out:

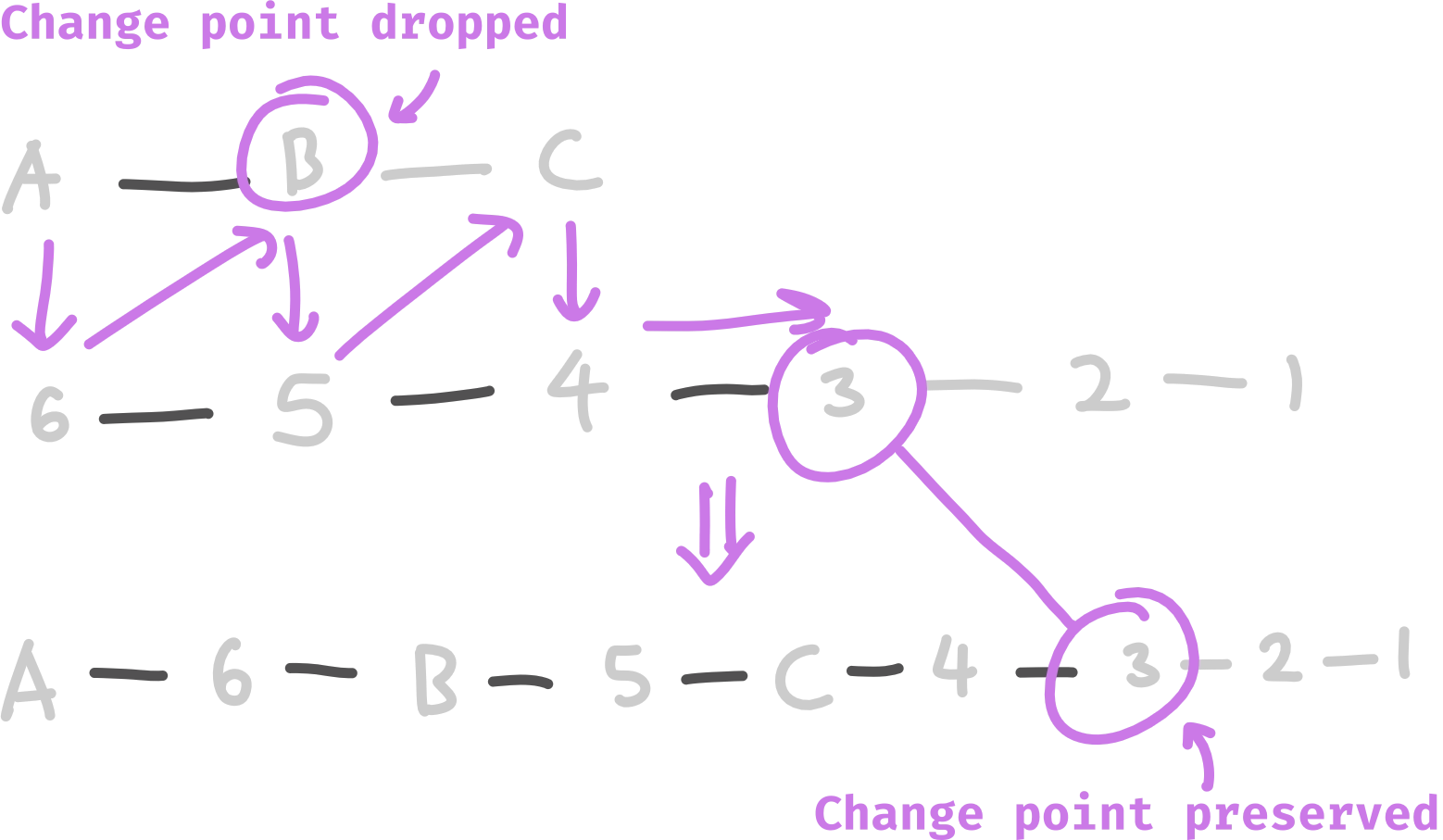
One more thing, this sequence puts node 1 at the end, since we call construct(1) to build the sequence. However, we want node 1 at the start, so we should reverse the sequence.

On a graph⌗

I soon realised, this problem generalises very elegantly from a tree to a graph.

Remember how the DFS tree of a graph guarantees that any non-included edges of the graph would go between a node and one of its ancestors? Guess what? There are no cross-edges between sibling subtrees in a DFS tree! This means that we can quite literally copy our code for the tree case onto the graph case, only needing a small modification.

construct(node):
    sequence = []
    for each neighbouring node c:
        if c has not been visited before:
            child_sequence = construct(c)
            sequence = combine(sequence, child_sequence)
    add n to back of sequence
    return sequence

There’s the solution!

…or is it?⌗

There are still a couple problems with our solution. I leave it up to you to solve these.

The combine operation, implemented naively, can be quite expensive (up to $O(n)$ time complexity, where $n$ is the number of nodes). This means that the algorithm runs in $O(n^2)$. Unfortunately, this is too slow for the problem. Can you figure out a way to do it in a faster time complexity? Hint: Use linked lists!
The graph provided in the problem doesn’t necessarily have to be connected. That is, not all nodes could be reachable from node 1. How can you extend this solution to allow for these cases? Hint: Can you invent a way of DFSing through an almost-complete graph with edges taken out?

If, after you have solved these issues, you feel comfortable implementing, I would strongly encourage you to give it a try. This link should take you to an online judge that can check your code.

Lastly, happy Halloween! (If it hasn’t already finished for you)